In Defense of Muon: A Deep Dive into Moonshot's K2 Optimizer (A Translated Analysis)

About the translation

This is a translation of the original blog post by toothacher17. The original post is in Chinese and can be found here. The author’s tweet about it is here. I translated it using Google Translate, Deepseek-R1, Gemini 2.5 Pro, and O3. This translation was edited by Kimi K2-Instruct at kimi.com.

Original Post

Author: toothacher17

Original Link: https://www.zhihu.com/question/1927140506573435010/answer/1927378524513219780

Source: Zhihu

Copyright belongs to the author. For commercial reprint, please contact the author for authorization. For non-commercial reprint, please indicate the source.

Disclaimer: Self-invited commentator, ex-Moonshot “No.1 Jiang Kernel hype-man” (might be duking it out with @Andrew Lu), Feilai Pavilion¹ stan and @苏剑林 disciple - shamelessly riding K2’s coattails for clout.

1. Concerns Around Using the Muon Optimizer

Moonshot’s freshly-dropped K2 was trained end-to-end with the Muon optimizer²³ – no AdamW safety-net. Muon was first proposed by Keller, crushed it on the Speedrun leaderboard², and then got the Moonshot treatment—some tweaks and serious scale-up^{3 4}.

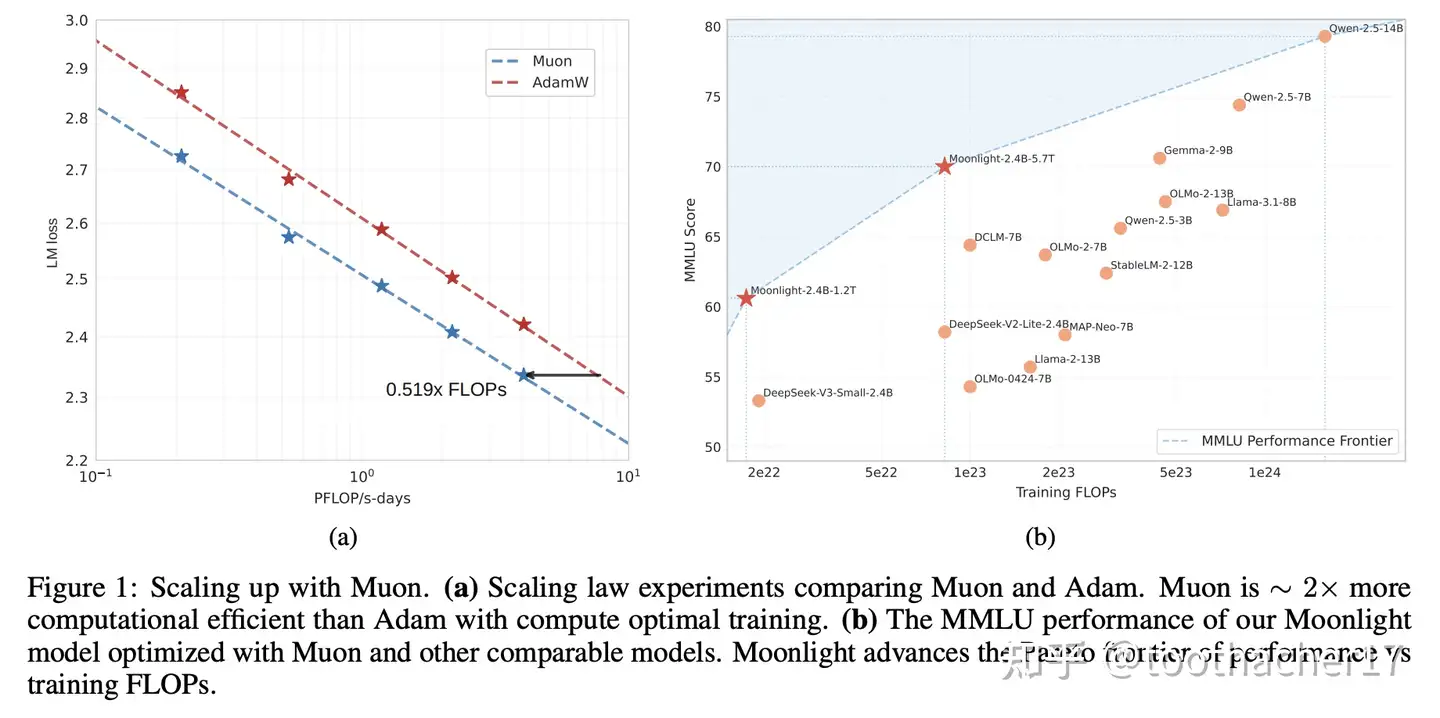
In Moonshot’s early tech report³ they claimed Muon brings god-level token efficiency and even open-sourced a Megatron-LM implementation⁵. Still, X (Twitter) was quick to throw tomatoes. Three memes keep resurfacing:

1. “Muon needs the whole parameter matrix for NS — RIP PCIe.” Muon requires the full parameter matrix for its “Normalized Stochasticity” (NS) calculation. In the parallel setting of modern LLM training infrastructure, many believe operating on the full parameter matrix is too expensive.

2. “Muon = more hyper-parameter sets = more pain.” Muon requires “several sets” of different hyperparameter tuning mechanisms, which places higher demands on model tuning—a stark contrast to AdamW’s “just one knob” simplicity.

3. “Muon training is a minefield—look at that attention logit blow-up!” Muon might cause training instability. For instance, Moonshot’s own paper³ mentioned a potential issue with the attention max logit.

With K2 now out, these fears seem less scary. This blog tries to quibble (狡辩) about why.

2. Concern #1 – “Muon Doesn’t Scale”

(TL;DR – we’re going to plug the hole the original Muon paper left about infra cost and prove it scales.)

First, let’s dig into whether operating on Muon’s full parameter matrix is truly that expensive, and in doing so, fill a small gap left in the previous paper³.

To get to the bottom of this, we’ll dive into Zero-1 sharding. Understanding its implementation—and the key differences between Chinese and international training clusters—is the only way to explain why Moonshot thinks Muon scales, while others on X remain skeptical. (And by “international,” we mostly mean foreign companies, who are so flush with cash and GPUs they have… different problems.)

2.1 Zero-1 Sharding Crash-Course

Modern LLM training relies on Zero-1 sharding (implemented in Megatron-LM/DeepSpeed/FSDP).

Zero-1 technology essentially shards the optimizer states—which consume a lot of GPU memory (e.g., AdamW’s exp, exp_square, fp32_master_weights)—across the Data Parallel (DP) group.

When using AdamW, the lifecycle of the Zero-1 Distributed Optimizer is as follows:

1. Gradient Reduce-Scatter: Perform a reduce_scatter of gradients between DP ranks. It’s a reduce_scatter instead of an all_reduce because of the sharding. Each DP rank only needs to ensure the gradients for the local parameters it’s responsible for are accurate.
2. Local Parameter Update: Perform the AdamW update calculation for the local parameters. Since AdamW’s calculation is element-wise, this step only needs to compute the updates for local parameters.
3. Parameter All-Gather: Perform a parameter all_gather between DP ranks. Because each DP rank only updated a portion of the parameters, an all_gather is needed for all ranks to get the complete, updated set of parameters. (Non-matrix params – word embeddings, lm_head, rmsnorm_gamma – stay on boring old AdamW.)

Note that steps 1 and 3, while seemingly communication-heavy, can actually be overlapped with the model’s forward/backward pass (a very mature technique all major frameworks implement), so there’s no need to worry. In step 2, since AdamW is element-wise and the computation per rank decreases as DP size increases, it’s highly scalable.

In summary, Zero-1 makes AdamW so cheap it usually eats < 1 % of global-step wall-clock – basically noise.

However, Muon faces a significant challenge in step 2 because its calculation is not element-wise. Muon requires the full parameter matrix to compute NS, which inevitably introduces additional communication and a larger computational load (running NS on the entire matrix).

For Muon to be as scalable as possible, the communication overhead of step 2 needs to be minimal (as it can hardly be hidden), and the additional computation introduced needs to be as small as possible (a single small matrix runs NS quickly, so we should avoid running NS on overly large or numerous matrices per DP rank).

2.2 The Moonshot Solution

Based on Moonshot’s open-source work⁵, it’s speculated that their development is based on a version of Megatron-LM that they have since maintained. For Megatron-LM, its early implementation of the Zero-1 optimizer⁶ is as follows (we’ll call it “flat-param concat zero-1”):

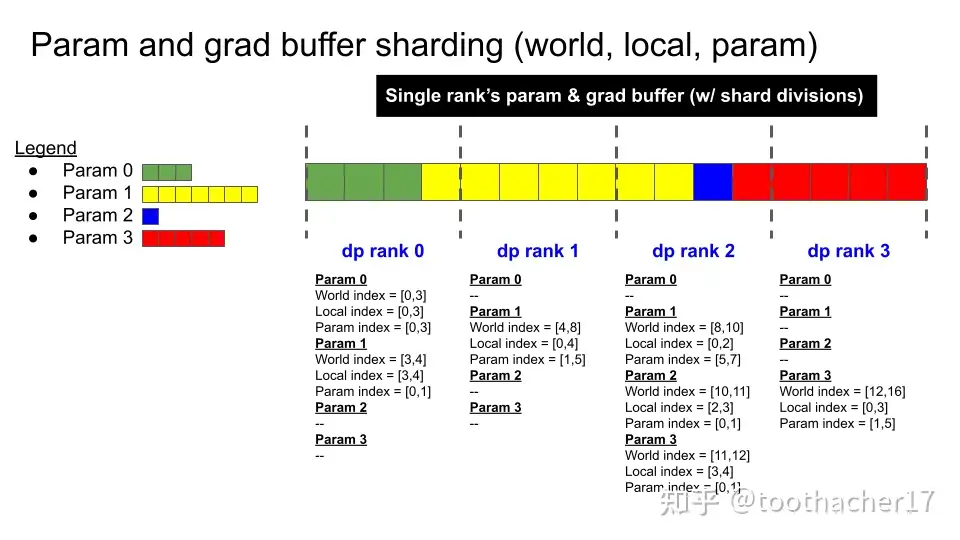
The approach is to flatten all optimizer states, concatenate them, and then distribute them evenly across the DP group. This allocation method is memory-optimal (no duplicate states) and highly Muon-friendly, since most local parameters remain complete matrices. Only the parameters at the DP boundaries get split across two ranks, requiring special handling.

Specifically, taking DP0 and DP1 jointly processing Param 1 as an example, if we were to brainstorm solutions, there are several approaches:

1. The “Brainless” Gather Method: DP0 and DP1 each perform a gather to get the full parameters. Both ranks then perform the full NS calculation. After computation, each rank only updates its local portion of the parameters and discards the rest. The grad_reduce_scatter and params_all_gather of steps 1 and 3 remain unchanged to avoid redesigning the algorithm.
2. Edge Parameter Passing: Each DP rank i sends its edge parameters to DP i-1. DP i-1 is then responsible for the computation on these edge parameters. After calculation, the result is sent back to rank i to update the portion it maintains. This avoids redundant computation, and the communication volume is actually better than the brainless gather method. However, for extreme cases, like a parameter spanning three DP ranks, this requires more complex heuristic arrangements.
3. Heuristic Precision Arrangement: When arranging the distributed optimizer, prevent the DP edge-splitting from happening in the first place. This eliminates any extra communication and computation. The cost is that memory allocation is no longer balanced, and finding the optimal allocation becomes a knapsack problem. Unbalanced memory allocation is obviously unacceptable for infrastructure engineers as it leads to inaccurate memory estimation during training, affecting the parallel allocation strategy.

In practice, Moonshot uses the brainless gather method because it’s simple and the overhead is tiny. The whole hack is ~10 LOC – infra teams cheer. Only the DP×2 edge slices need this treatment; all other parameters are complete and don’t require any extra work.

Empirically, the overhead is negligible because modern MoE architectures (thanks, DeepSeek-V2) don’t have single, monstrously large matrices. Instead, they use many fine-grained experts (and things like word embedding/lm_head are handled by AdamW, not Muon). Therefore, in the long run, Muon’s scalability has a bright future.

Since the cost of the brainless method was already so low, the ROI on engineering a fancier solution was minimal, so “Jiang Kernel” had no motivation to continue optimizing (though I remember You Jiacheng might have implemented some similar hacks on Speedrun?).

2.3 Others’ Concerns

However, in the research from some foreign companies, there is a pessimistic bias towards Muon’s scalability^{7 8 9 10}, and Moonshot’s method⁵ has been repeatedly criticized. Obviously, it’s not that everyone else is an idiot. But based on the analysis in 2.2 and the fact that Moonshot successfully trained K2 at a large scale, Moonshot isn’t an idiot either.

I personally believe the main reason for this conflict is the different implementations of Zero-1, which leads to a large discrepancy in the estimated overhead of Step 2.

The mainstream method abroad is called dim-0 sharding Zero-1. For example, the Zero-1 implementation in the mainstream foreign parallel framework, PyTorch FSDP2, is as follows¹¹:

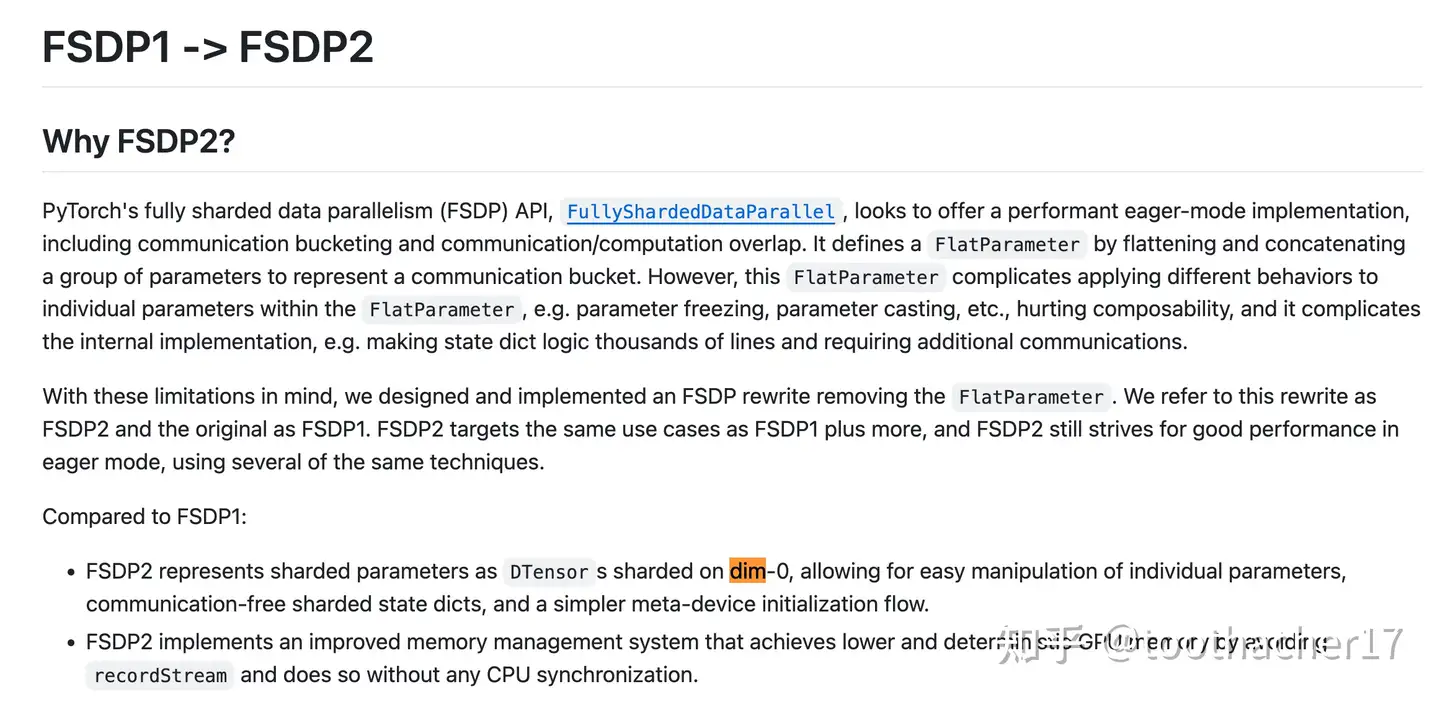
And a newer version of Megatron-LM¹² introduced the concept of “buckets.” The essence of this concept is similar in effect to params dim-0 sharding:

These updates are a “devastating” blow to the Muon implementation that preceded Moonshot’s work. This type of Zero-1 implementation causes every parameter to be sharded by DP. The methods we discussed, all based on “flat-param concat zero-1,” are completely ruined. Every parameter now requires communication and redundant recalculation, leading to a massive amount of extra overhead – Muon is basically DOA under dim-0 sharding.

2.4 Long-Term Solution

Foreign companies are definitely not stupid. Early parallel designs actually all used flat-param concat zero-1¹³. Later, due to other concerns (mainly that foreign companies have too many GPUs, and flat params are not conducive to overlapping grad_reduce_scatter and params_all_gather), they switched to dim-0 params sharding Zero-1.

In the context of mandatory dim-0 params sharding, the Moonshot method is indeed not scalable. But this does not mean Muon is inherently unscalable. New solutions will definitely emerge. In fact, I’ve heard that it seems possible, and someone might already be working on it 🐶.

3. Concern #2 – “Muon needs more hyper-parameters”

Another common complaint is that Muon has several sets of hyperparameters, which is seen as a significant disadvantage compared to AdamW:

1. It requires additional tuning efforts.
2. The need for extra tuning means more mental overhead to find the best model, which isn’t a fair comparison to AdamW.
3. If AdamW were also tuned in blocks, it might achieve better results.

I personally think this concern stems from a lack of precise understanding of the mathematical properties of the Muon optimizer. To understand Muon, we need to look at it from the perspectives of Standard Parametrization (SP) and Maximal Update Parametrization (µP) to see why multiple sets of parameters need adjustment.

Additionally, Muon is designed for matrices². Non-matrix parameters like word embeddings, lm_head, and rmsnorm_gamma are all updated using AdamW.

3.1 Standard Parametrization (SP) + Muon

Let’s first look at Muon under SP. When Moonshot started researching/reproducing (copying) Keller’s Muon in the early period (around December 2024)¹⁴, it looked like this (without weight decay and without the various engineering optimizations added by Mr. You, like the zero-1 optimizations):

At this stage, there weren’t so many outrageous sets of parameters—just one set for AdamW and one for Muon. However, the update RMS (Root Mean Square) of Muon is very different from that of AdamW. In Moonshot’s work³, Su Yin provided a derivation:

This shows that AdamW’s update RMS is empirically around 0.2-0.4, while Muon’s is much smaller. If you don’t increase Muon’s update RMS (the simplest way being a dedicated learning rate), Muon simply won’t update effectively, making it an unfair comparison.

In the SP setting, if you don’t want to tune two sets of parameters, you can directly use Moonshot’s work³. By matching the update RMS, it’s practically “out-of-the-box.” You can use a single set of AdamW hyperparameters. There’s plenty of work on how to tune AdamW hyperparameters (e.g., the stepfun law). Moonshot’s adapter means you can literally copy-paste any AdamW LR schedule and call it a day. Just copy one and migrate it to Muon using Moonshot’s method, and you will likely get good improved loss token efficiency.

In fact, the main contribution of Moonshot’s work is here: allowing everyone to migrate to Muon in the SP setting without much thought. My superficial understanding is that this is equivalent to the fastest optimization under a matrix Frobenius norm constraint, which effectively controls the update RMS, similar to AdamW. It meets the requirements of SP, but it’s not optimal. For Muon, the theoretically optimal method is the fastest optimization under a spectral norm constraint, which we will discuss next.

3.2 µP Parametrization + Muon

The most exciting use of Muon is not SP, but its combination with µP (Maximal Update Parametrization). A series of open-source works have provided very exciting introductions! [^16 ]^{15 16}.

In short, Muon is almost an optimizer tailor-made for µP. Unlike using µP + AdamW, which introduces many variance-based assumptions, Muon naturally controls the spectral norm (because NS mathematically clips the max singular values, and the max singular value is the spectral norm by definition). This makes it perfectly suited for the spectral norm control required by high-order µP¹⁵!

Looking at Keller’s improvement history on Muon, besides infrastructure optimizations by masters like Mr. You, the main evolution was the introduction of µP ideas by Jeremy Bernstein (Jeremy is an author of both µP and the Muon blog, so he’s double god-tier).

After introducing ideas similar to µP, the Embedding, LM Head, and Hidden Matrices all got their own control logic¹⁷. Although it seems outrageous, it’s reasonable when you consider the need to adapt to µP (in fact, adapting AdamW for µP also requires learning rate adjustments for different modules).

In particular, look at the adjustment of Muon’s update RMS here. Ignore the max(1, x) part for a moment and just look at the sqrt(d_out/d_in) part. This is exactly the same as the derivation in Su Yin’s high-order µP blog¹⁵! (Though I don’t know why the max(1, x) operation was added. With max, it actually reverts to a Frobenius norm-like scaling, doesn’t it?)

4. Concern 3: Muon Training Instabilities

In reality, few companies train Muon at truly large scale. Moonshot themselves report only two instability sources^{3 18}:

1. Weight decay.
2. The max attention logit problem (addressed by muonclip).

Weight decay is easy to understand, while the max attention logit problem involves the muonclip method mentioned in their recent blog¹⁸.

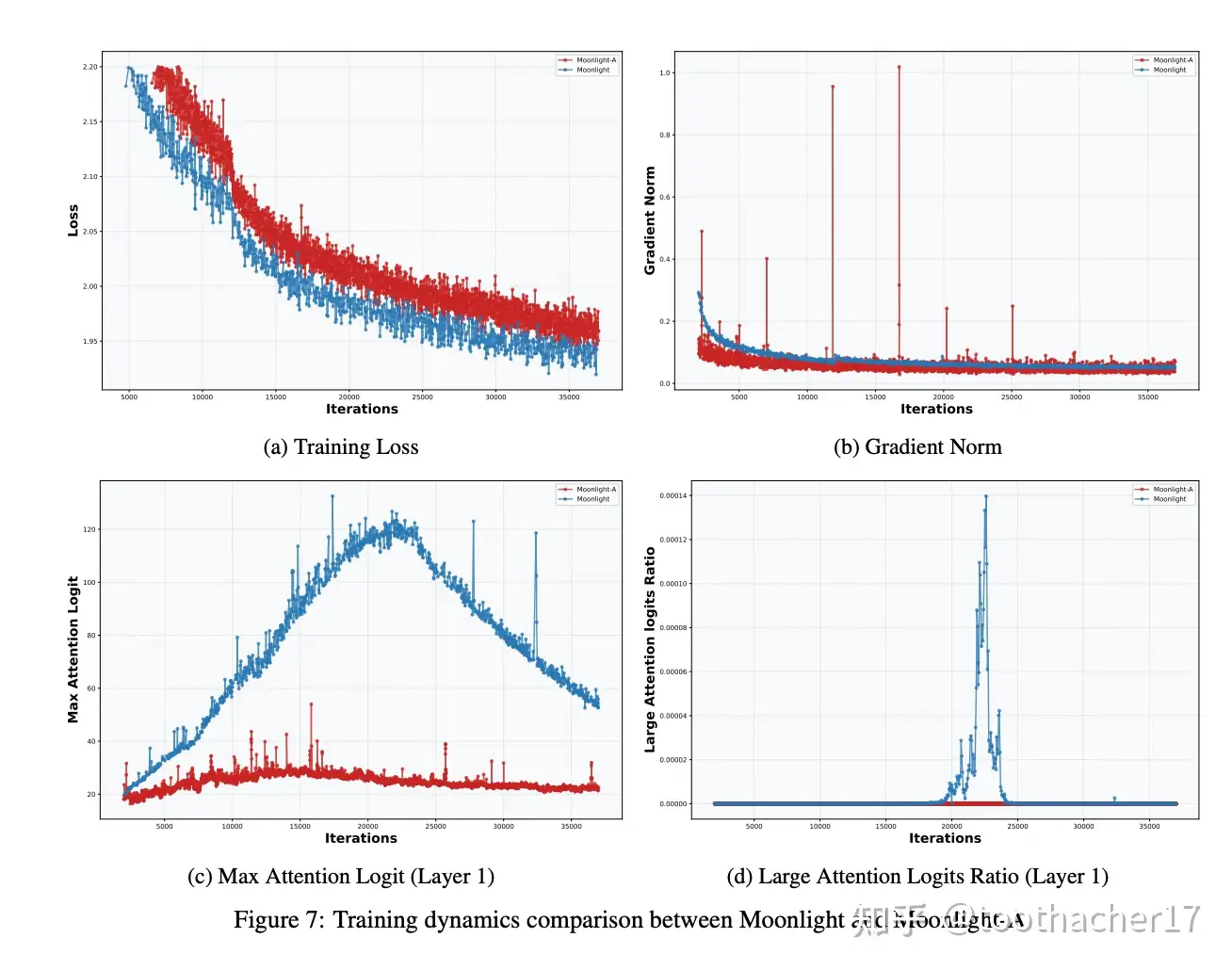
The max attention logit problem can usually be solved with qknorm, but Moonshot used MLA (Multi-Head Latent Attention) in K2 (I have to say, DeepSeek is ruthless; their model architectures are tried-and-true winners). The results are probably just that good, so there’s no need to force innovation when a great technology already exists. MLA adds normalization during compression, but for inference efficiency, the q and k heads aren’t materialized, which means you can’t perform qk-head normalization.

Therefore, Moonshot took a different approach and created muonclip (in fact, others have also expressed concerns about the effectiveness of qknorm¹⁹).

I personally find muonclip very elegant! In Su Yin’s high-order MuP blog¹⁵, we learn that the spectral norm is smaller than the Frobenius norm:

And the spectral norm is directly tied to the maximum logit size, i.e.

||x W||₂ ≤ ||x||₂ · ||W||₂

(where W is a matrix, so ||W||₂ is its spectral norm). The most direct approach is to control the spectral norm. However, the spectral norm is difficult to calculate. So, we can use the inequality relationship between spectral and Frobenius norms and directly clip the Frobenius norm. By doing so, ||xW||_2 will be controlled!

But later I had a chance to chat with Su Yin, and he said he didn’t think that far ahead, and my understanding might not be right (人麻了). His idea was to directly operate on the fundamental problem. Su Yin mentioned he will be releasing a blog post in the next few days, so keep an eye out for that.

5. Conclusion

K2 is shaping up to be cracked.
Moonshot already crushes VL + RL; once they stack thinking + vision on K2, expect fireworks.

With Su Yin, Jiang-kernel, and Feilai-Pavilion’s Zhang Yu on the roster, Moonshot’s ceiling is sky-high.
A company that ships Muon and happily borrows DeepSeek’s MLA? That’s big-dick energy.

Footnotes